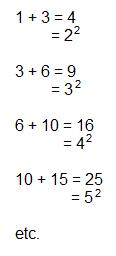Introduction
=============
Number
Sequences
=============
Number Series
=============
Fibonacci Sequence
=============
The Ultimate
Triangle
=============
Credits
=============
Garden 2: Gauss' Butchart

Hey friends we have entered a flamboyant garden--it includes a variety of more fancy and dazzling stuff that may look complicated at the first glance, but actually isn't that bad when we settle down and savour it... So let's begin!
We'll be applying our knowledge of sequences to more sophisticated stuff and
observing some fascinating phenomenon of patterns in math.
Our first topic is going to be series.
"A series is the sum of all terms in a given part of) a number sequence of any kind."
We'll be only dealing with arithmetic series.
| {1,5,9,13,17,...} | This is a sequence |
| {1+5+9+13+17+...} | This is a series |
Sn is the symbol we use to represent the sum of all of the terms up to the nth term of the sequence--which is essentially "series".
- Arithmetic Series
Q: When Gauss was a small child an adult in the house asked him to find the sum of 1 to 100 to keep him out of the way. Instead of spending hours doing the "proper arithmetic", however, Gauss found the RIGHT answer in less than a minute. Now it's YOUR turn! ...Except that you only have to find the sum of numbers 1 to 12:
A: ...Well how simple's that?
1 + 2 + 3 + 4 + 5 + 6...
...Are you feeling all right there? How's the answer?
?#*^!%!@$()??????
...Exactly!!
It is easy to get lost in such a maze, but there's a pathway... let's try using 2 sets of the sequence and add them up
vertically:
S12 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12
+ S12 = 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
_________________________________________________________________
2S12 = 13 + 13 + 13 + 13 + 13 + 13 + 13 + 13 + 13 + 13 + 13
2S12 = 12(13)
2S12 = 156
S12 = 78
We can also look at it as:
Sequence { a, a+d, a+2d, ... tn-2d, tn-d, tn }
or { tn, tn-d, tn-2d, ... a+2d, a+d, a }
_____________________________________________
a+tn,a+tn,a+tn,... a+tn, a+tn, a+tn
The formula that we can use to calculate series looks like this:
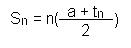
Or we can express it as this:
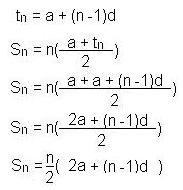
- Busy Bee Exercise
Q: Find sum of the following arithmetic sequence:
{ 4, 1, -2, -5, -8, ... -1703 }
A: Since we don't know the value for n, we'll bring in the formula for the arithmetic sequence:
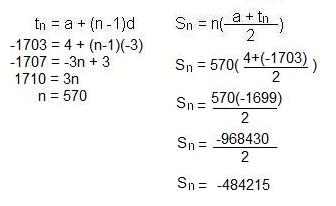
Q: Find S62 for the following arithmetic sequence:
{ 3, 8, 13, 18, 23, ...}
A: This question is just simple substitution! But since we don't know the value for t62, we HAVE to use the formula:
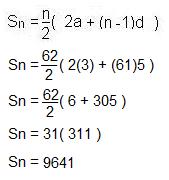
- Triangular Numbers
"A triangular number is the sum of "n" number of natural numbers from 1 to value n."
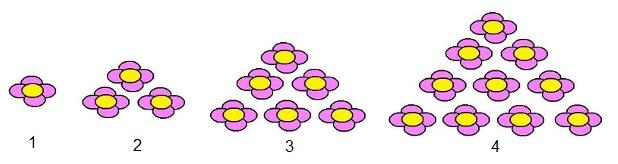
...What a beautiful pattern! Notice that the number of flowers in each of the patches can form an "equilateral triangle" which has the same number of flowers on each side. This is a sequence, which looks like:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| tn | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | ... |
Realize that tn is equal to the "series" of natural numbers ("counting numbers", like 1, 2, 3, 4, ... but WITHOUT zero) up to value "n":
| {1, 2, 3, 4, 5, 6, ...} | The sequence of natural numbers |
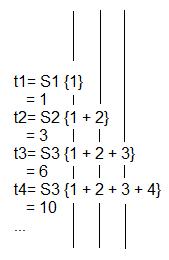
Tell me immediately, what number comes next?
There's a quicker way to go about it than doing series calculation every time. Watch:
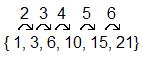
So if I ask you what comes right after t4 which is 10, you can automatically add 5 and get 15.
t5 ... add 6
t6 ... add 7
And so on.
- Garden Highlight
-
Do you know that ANY natural number can be the sum of either 2 or 3 triangular numbers? Check this out:
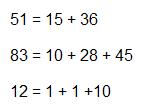
Also, the sum of 2 adjacent triangular terms is equal to a perfect square: