Garden Last: Pascal's Palace

• Pascal's Triangle

Hush friends! We are about to enter a palace--a pure-white palace built entirely out of white marble bricks. The architecture's Gothic style is absolutely breath taking; yet there are more to expect inside!

Here is the key to the gate of our last garden--we're being greeted by a tall "pyramid"--or triangle, rather, made of white marble cubes. This is a pattern!

...Let's do something with this pyramid. Starting with 1 at the top, we'll fill in the pyramid with the sum of the 2 cubes directly above.

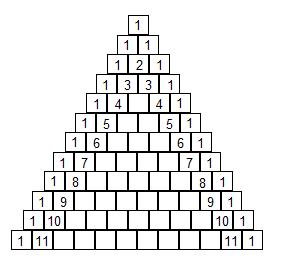
What? Too much? Not at all! What have you noticed? A pattern is occurring... beside the diagonal lines of perfect 1's, we have diagonals of 1, 2, 3, 4, 5,... Keep going! That's the beauty of patterns--what looked like a spider is actually honey for no-brainers!
WHAT'LL HAPPEN NEXT?

We've filled in the entire triangle now! But we're just starting. This triangle is called the Pascal Triangle, and by simply writing in the sum of the 2 cubes right above, it forms a great number of sequences and pictorial patterns within itself:

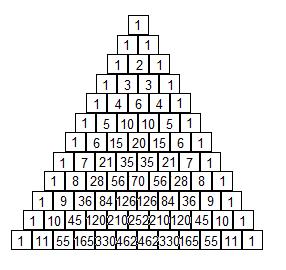
• Garden Highlights

1. Diagonal Rows 1, 2 and 3

Row 1 down both sides of the triangle from the top is straightforward--they're all 1's!

Row 2 is the sequence of counting numbers or natural numbers.

Row 3: 1,3,6,10,15,21,... sounding familiar?? Yes, THE TRIANGULAR NUMBERS!!!

2. Horizontal Rows

Check out the following:

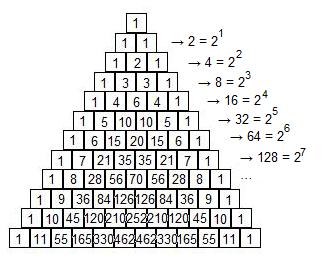
If we add up all of the numbers in a horizontal row starting at row 2, the answer would always be equal to the power of 2.

3. "The Fib"

Let's try some more additions... We'll start with the first square:
1
And find the sum of each DIAGONAL ROWS as shown in the picture this time:
1
1 + 1 = 2
and so on:
1 + 2 = 3
1 + 3 + 1 = 5
1 + 4 + 3 = 8
...

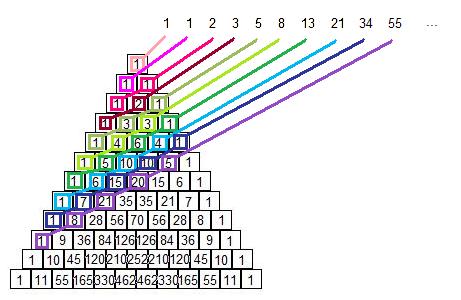
{ 1, 1, 2, 3, 5, 8, 13, 21, ... } There's the Fibonacci Sequence in the Pascal Triangle!

4. Triangles within Triangle

Find all of the even numbers in the triangle and highlight them:

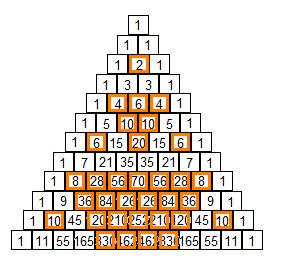
They all form upside-down triangles (the single-square can symbolize a point, which in turn can symbolize a very small triangle)! Hence, the number of cubes in each of these small triangles is triangular numbers!
Let's try highlighting numbers divisible by 5:

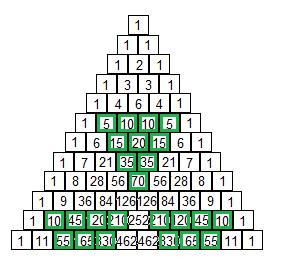
Tadaaa! More sets of triangles!!!

You can also try the divisibles by 3 and 4 and check out the patterns they create on the triangle!

Top of Page