Introduction
=============
Number
Sequences
=============
Number Series
=============
Fibonacci Sequence
=============
The Ultimate
Triangle
=============
Credits
=============
Garden 1:
Jack and the Beanstalk
- Arithmetic Sequence
"An arithmetic sequence is one in which the difference between successive terms is constant."--N. Johnson
The stem of Jack's beanstalk grows 5cm every minute:
{5,10,15,20,25,30,35...}
Notice that the difference between each term is 5
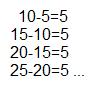
...The growth of the Beanstalk is an arithmetic sequence!!!
- General Rule
What is the general rule for the pattern of Jack's beanstalk?
a represents t1
d represents the COMMON DIFFERENCE between each term
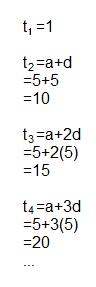
From here we can conclude that
tn=a+(n-1)d
- Busy Bee Exercise I
Q:Find the general term, tn and t32, for the
following sequence:
{4,7,10,13,16,19,...}
A:tn=a+(n-1)d
tn=10+(n-1)5
t32=10+(32-1)5
=10+(31)5
=10+155
=165
Q:How many terms are in the following sequence?
{-4,-1,2,5,...332}
A: In this case we're asked to solve for the number of terms,
which is n:
tn=a+(n-1)d
332=-4+(n-1)3
336=3n-3
339=3n
n=113
Q:Find the missing terms in the arithmetic sequence:
{...23,__,__,__,75,...}
A: Since the arithmetic sequence is consistent all the way through,
we can just take the part of the sequence we are given information for and
pretend that our sequence simply begins with 23 and ends with 75. Now it's
just simply substitution!
tn=a+(n-1)d
75=23+(5-1)d
52=4d
d=13
Now we have the difference between each term, it's easy to figure out the
missing terms:
23+13=36
36+13=49
49+13=62
{...23,36,49,62,75,...}
What we've just done is called finding the arithmetic means of the sequence.
- Geometric Sequence
"A geometric sequence has each successive term increasing by a 'common ratio'. --N. Johnson
Look at the example below:
{1,3,9,27,81,243,...}
Realize that the terms increase very quickly in size and certainly do not form anything like an arithmetic sequence.
However, also realize that:
3/1 = 3
9/3 = 3
27/9 = 3
81/27 = 3
243/81 = 3
...
The "common ratio" between each term is 3!
- Busy Bee Exercise II
Q:Find the common ratio for the following geometric sequence:
{13,-13,13,-13,...}
A:Since it's a geometric sequence, we can just take any 2 random
terms adjacent to each other and divide (although either order would produce
the same result in this example, always divide the term by the one after it.
-13 / 13 = -1
The common ratio for the geometric sequence is -1.
Q:Find the first 5 terms for the following geometric sequence:
t1=2.5, r=3
A:...This is sooooo straightforward!!!
t1=2.5
t2=2.5 x 3 = 7.5
t3=7.5 x 3 = 22.5
t4=22.5 x 3 = 67.5
t5=67.5 x 3 = 202.5
{2.5,7.5,22.5,67.5,202.5,...}
Q:Find the next 3 terms of the geometric sequence:
{0.2,1,5,...}
A:Before we go any further, we must find the common ratio for the sequence
5 / 1 = 5
(Always take the most obvious approach)
...Now what???
5 x 5 = 25
25 x 5 = 125
125 x 5 = 625
{...25,125,625,...}
Q:You have been shown the method of approaching a general rule for a sequence. Now find the general formula for a geometric sequence (in terms of tn) on your own!
A:Let's begin by making up a geometric sequence! All you need is a starting value (t1) and the
rate (r) which is the common ratio. For example:
t1=1,r=2
Then it's easy to figure out all of the terms' relationship to t1 by including the 1, our starting value,
in each calculation of the term AND using ONLY our r value to get the answer:
| n | Regular Calculation (tn-1)(r) | Calculation using only t1 and r |
|---|---|---|
| 1 | 1 | 1 |
| 2 | (1)(2) =2 |
(1)(2) =2 |
| 3 | (2)(2) =4 |
(1)(2)(2) =4 |
| 4 | (4)(2) =8 |
(1)(2)(2)(2) =8 |
| 5 | (8)(2) =16 |
(1)(2)(2)(2)(2) =16 |
Realize in each "Calculation using only t1 and r" column we end up using
- the t1 value ONCE
- the r value ONCE LESS than the nth term
...our equation can thus be described as:
tn=arn-1
Q:With the formula you've come up with in the previous question, find the 3 geometric means for the
following sequence:
{...1.25,__,__,__,3001.25,...}
A:We need to find the r first, which is just simple substitution!
tn=arn-1
3001.25=1.25r4
3001.25 / 1.25 = r4
4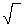
2401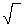= 4r4
r = 7
Then...
1.25 x 7 = 8.75
8.75 x 7 = 61.25
61.25 x 7 = 428.75
{ 1.25 , 8.75 , 61.25 , 428.75, 3001.25,...}